what determines the ring output?

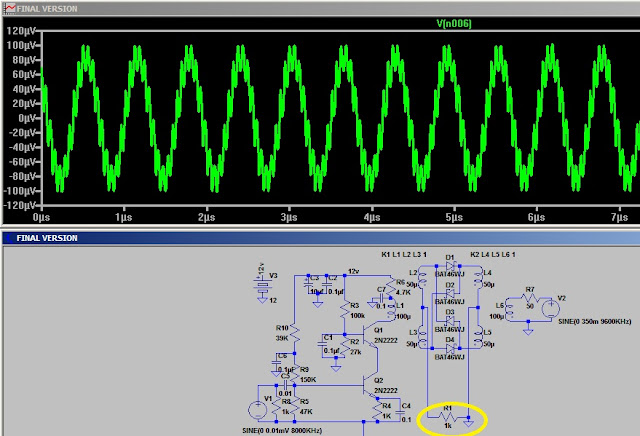
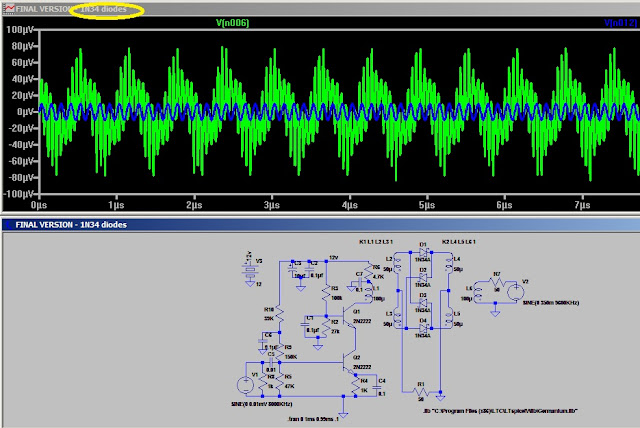
Now the question is "what's going on in the ring and how to 'match' it?".  When I made the secondary half what it was the output responded so the next step was to reduce it more. It seems the diodes need more current.

 In spice you can open the window menu and select set reference to set the negative probe. Here I set the probe at the center tap on the secondary. I measured the top of L2 and ground and that equals the output so whatever is on L2 - l3 is equal the output.

Consider the diode characteristics

These datasheets are available in a couple of different places. They were developed by Ben T. and Mike T.

They show a thing called Ideality factor or N on the chart. In theory 1.000 is ideal. Look at n and Ro.

I did a little cut and paste to isolate the diodes we have been using in out sims.

Using Avago's design program to compare n at 1,2,3,4

If you compare 0db you will see n=1 is the highest output. Looking back at the chart you can see the BAT46 has n=1.1 and the IN34a n=1.3 yet the 1N34A output soars? Look at Ro. The 1N34A is 35 - 40K while the BAT46 is 175-100K. Could it be the lower Ro? Look at the D18 with Ro of 160-170K it soars?

So that brings me back here. I put reference at L2 - L3 and measure to the other end of the coils and then to ground. The output is = the voltage across L2 & L3. When R1 is about 40K the output peaks. Lowering R1 will lower the output but raising R1 has no effect on the output. 

 Food for thought.

DBM BAT-46 vs 1N34A

I have some questions about the diode selection and the feed to the AF amp so a couple of quick sims.

BAT46 diving a 50 ohm load. (45uV)

BAT54 driving a 1K load (100uV)

1N34A driving a 50 ohm load (80uV)
Now for a surprise???

1N34A driving a 1K load at plum new 1 mV. All I changed was the diodes and the load resistor and we go from 45uV to 1 mV. The 1N34 was developed to be used in radar some maybe it should not be a surprise that it would function well but what just happened? That thing about Z matching from a couple post back. The 1N34A is 40 - 50k Z while the BAT46 is 200K.Just to test/prove the point I put a couple 100k resistors across two diodes and .

Notice the negative is unchanged. So armed with this info I'll try some different diodes and output loads.

The BAT54 with a higher Zo is more respectable.

D18 diode at 5K. looking good

The 1N34A at 40k

As a final check, the 1N34A at 400K. Notice once the load goes above 40K we see little change. So now the question is do we have some 1N34As or D18s if not how to match the output?

Toroid Calculator

toroid calculator

The toroid data is in the program for a lot of common cores AND it has an unknown core function.

zipped calculator


I zipped the program so you can download it.

Transformer for the DBM.

In my earlier short ramble the question was how much inductance do we need? First stop in search of the answer was the catalog. notice the larger coils have lower frequency limits. The most common practice is to use a trifilar wound toroid with a few turns maybe 10 - 12? (I think I saw one with 7 turns) Part of that would depend on the core. We also need to consider the Z matching, does it serve a useful purpose to dissipate half the power in the generator? How much current do we need to switch the diodes? Looking at the charts tells us we could use less than 100uh for MW. I'll just post some test and we can look at them to decide how much of my ramble is worth considering.

With 700mv driving a 1mh coil we lose more than half our signal inthe generator drop and we are driving with 4ma. Thus my question, how much drive do we need?

Here I set the reference at +V2 so we can see the drop across R7.

 With 10 uh coils the signal is still strong but the current is still 4ma.

 Here I cut the drive to 350mv and the output went UP to 45uv with 1 ma in the coils. Notice the transformer. I did not use a trififar winding. the secondary is equal to the primary. The step down transformer provide higher current and reduces the load on the LO.

 Here I had lowered the drive and got less loading on the LO with the output holding level.

 Another look at the generator lose. the red is the drop across the 50 ohm resistor.

Another look at the original circuit. 700mv drive and 300mv across the coil with 4ma in it. Now what did I find out with all this that we may be able to use?

I lowered the drive to 350mv and center tapped the secondary coil at 100uh.I now have 300mv across the coil and 1ma current in the coil. What about the output?

45 uv out.
So it is time to wind a new transformer. If not trifiliar then how?

How much inductance does a DBM transformer need?

In a day gone by I was taught the source Z should be 1/10th the load Z. It seems common knowledge today is Zs=Zl for max power transfer. When I was a teen the books said you get max power when Zs=Zl and your generator/battery consumed 1/2 the power, for this reason we set Zl at least 10 times Zs. With the 10 to 1 ratio we still use 9% heating the source. With that in mind and looking the manufacturer datasheets I decided to do a none scientific test using spice to see if I can find the 'perfect' transformer. Andy sent me a circuit which I used for the test. Then I built a circuit and tried it. Here are the circuits used in the test:

 my circuit.

Andy's circuit.

The results:

100 uh 10 uv in 15 uv out

1uh 10uv in 15 uv out

It was looking like it could not go to low so 1ph no output.

I looked through several spec sheets and found coils wound wit 3 turns, 6 turns, etc. The only spec they gave was the Z at a certain frequency. The recommendation was for the transformer Z to be 4 times Zs at the lowest frequency. The test seem to support the fact that more inductance doesn't give more output. It did show that some of the circuits drew a larger current and loaded the source more.

The DBM with homemade transformers

Making a DBM using trifilar wound coils.

I gathered all the parts. I'm using a microscope slide as my base. I covered the top of the slide with copper foil. I'll be using 10 meg ohm resistors as my stand offs. The two cores are wound with 11 turns of 3 twisted wires. A piece of solder, 4 diodes and some rivets complete the list.

I soldered a rivet to ground and one on a standoff at each end for the Rf and LO connections. Four rivets on standoffs for the diodes. Then put the  diodes in a diamond, head to tail.

I put 2 tie points for the output AF and install the transformers.

The DBM and the hearing aid amp are ready to test.

Here is a closer view of the DBM.

The second generation oscillator

Putting the second generation oscillator on board

I printed the circuit out.

Number all the points. Zero is ground and then just number the tie points.

I put down copper foil for ground and screwed terminal in for the tie points. I numbered them to try and not get confused. Then it was tie the components between the tie point while referring to the drawing.

After wiring it up I put 6.2 volts on it and got 383 mv Pk-Pk with a one turn feedback.

The second version of the oscillator using 2N2222 transistor

Andy's oscillator version two

I 'built' the oscillator in spice with good results. I did discover to much feedback is easy to obtain. If you step L2 up in value it will not be long before you discover its limit. I took a short lead and made a single turn coil in the core I intend to use and it had .3uh so there will be a need to not be to zealous with the feed back winding. 2 or 3 turns should do.

Playing with the RF Amp in spice

The sim will run faster if you set the display time to a smaller value. I made that change and will point it out when I post the picture. That run took about 5 minutes to load before I changed the setting. Ok back to the DBM LO requirement.

The level 7 will be .7 volts peak. Now let's look  at the oscillator.

I have built the one on top of the page. I plan to try the other when I get some shop time. The one I made produced about 250 mv so it will need a little boost. I posted the  model for a RF amp in my last post. The last line in the post. The questions are will it produce the output level we need and at what frequencies will it function. If it works as desired we can build the oscillator for the frequency range we want to receive.

Notice I set the input at 50 mv and 10mhz. So at 10 mhz we should see greater than .7 volt peak.

At 20 mhz it has dropped off a bit but still good.

At 30 mhz dropped some more but still good. Note the orange circle. It took 5 minutes to run this sim and I lowered the time for the viewing window. With the new times it loads in less than a minute. Shortwave is generally 3 - 30 mhz so it should be good for our set but I had to do one more test to push it limit.

At 100 mhz it is still providing some gain.
The transformer I'm using in the sim is a tri-coil supplied by BG Micro. The little coil is 25 cents each and works well. You can wind your own but will have to adjust the values to fit. I wound a Fair-Rite T50-43 with 11 (trifiliar) turns and it measures 60uh per winding. Substituting the value for the transformer will tell the story about the transformer requirements. That will be a project for later.
NOTE: I made a DBM with the Fair-Rite cores and 1SS98 diodes and it did function when driven with my signal generator.